Blog

Wie unterscheiden sich die Monte-Carlo-Simulationen von Portfolios in Abhängigkeit von verschiedenen Wahrscheinlichkeitsverteilungen der Renditen?

Die Realität, die wir erleben, ist nur eine Manifestation einer unendlichen Anzahl verschiedener Pfade. Diese Annahme bringt man eher mit einer philosophischen Grundsatzdebatte oder der Viele-Welten-Interpretation der Quantenmechanik in Verbindung, aber nicht unbedingt mit einer der Standardmethoden der Finanzindustrie. Die Rede ist von der Monte-Carlo-Simulation. Diese werden wir in diesem Artikel beleuchten und ein Online Tool vorstellen, mit dem ihr selbst mögliche Zukunftsszenarien für euer Aktien-/ETF-Portfolio simulieren könnt.

Das Vorgehen bei der Monte-Carlo-Simulation wurde bereits im Jahre 1949 von den Wissenschaftlern Metropolis und Ulam veröffentlicht. [1] Sie ist eine Methode der Mathematik, bei der eine große Anzahl von Zufallsexperimenten gemäß einer Wahrscheinlichkeitsverteilung simuliert wird. Aus den Ergebnissen ergeben sich dann mögliche Zukunftsszenarien.

Um den Prozess zu veranschaulichen, können wir die samstägliche Lottoziehung als Monte-Carlo-Simulation in der physischen Welt betrachten. Dabei entspricht das Ziehen einer Lottokugel dem oben erwähnten Zufallsexperiment. Da bei der Lottoziehung aber nicht nur eine einzige Kugel, sondern sechs Kugeln gezogen werden, besteht die Simulation eines möglichen Szenarios bzw. Pfades aus dem sukzessive Ziehen von sechs Kugeln. Wiederholen wir diesen Vorgang mehrfach, ergibt sich ein Korridor von möglichen Zukunftsszenarien und daran kann man ableiten, wie wahrscheinlich ein bestimmtes Szenario ist.

Bei dem Lottobeispiel wäre das Ziehen von „sechs Richtigen“ ein Extremszenario, weil nur sehr wenige Pfade zu diesem Ergebnis führen, während das Ziehen von keiner richtigen Zahl am wahrscheinlichsten ist, da die meisten der Pfade in solch einem Ergebnis resultieren. Man sollte somit zum Entschluss kommen kein Lotto zu spielen. Neben diesen „Simulationen“ in der physischen Welt, können Monte-Carlo-Simulationen mit einer großen Anzahl von Szenarien mit Computern simuliert werden. Das Lottobeispiel werden wir weiter unten wieder verwenden, um das Vorgehen bei der Simulation von Aktienrenditen zu beschreiben. Statt mit einer Lottozahl kann jede Kugel auch mit einer monatlichen Rendite beschriftet werden. Dann würde das Ziehen einer Lottokugel dem zufälligen Bestimmen einer monatlichen Rendite entsprechen.

Welche Voraussetzungen müssen nun bestehen, um die Entwicklung des Aktienmarkts mit Hilfe der Monte-Carlo-Simulation zu simulieren? Zunächst müssen wir annehmen, dass die Kursentwicklung des Aktienmarkts zufällig ist. Diese Annahme ist unter Wissenschaftlern weit verbreitet, aber nicht unumstritten. [2],[3] Gehen wir aber von dieser Annahme aus und kennen wir die den Renditen zugrunde liegende Wahrscheinlichkeitsverteilung, können wir die mögliche Entwicklung des Aktienmarktes simulieren. Ist die Anzahl der simulierten Szenarien groß genug, lassen sich daraus aufschlussreiche Erkenntnisse gewinnen.

Die Renditeverteilung von Aktien

An die Aufgabe eine Wahrscheinlichkeitsverteilung für die Renditen des globalen Aktienmarkts zu bestimmten, haben wir uns bereits im letzten Blogeintrag Rendite von Aktien und ETFs der letzten 50 Jahre gewagt. Dabei haben wir die Daten des MSCI World der letzten 50 Jahre verwendet und daraus eine Normalverteilung abgeleitet, die eine im Großen und Ganzen gute Beschreibung der Renditeverteilung liefert. Jedoch werden Börsencrashs mit stark negativen Renditen wie z.B. die Dotcom-Blase oder die große Finanzkrise signifikant unterschätzt. Die Verteilung der Rendite ist nämlich asymmetrisch bzw. schief und weist für stark negative Renditen einen sogenannten „Fat Tail“ auf. Die monatliche Renditeverteilung des MSCI World sowie die daraus abgeleitete Normalverteilung mit einem Erwartungswert von 0,87 % und einer Standardabweichung von 4,3 % sind in Abbildung 1 dargestellt.

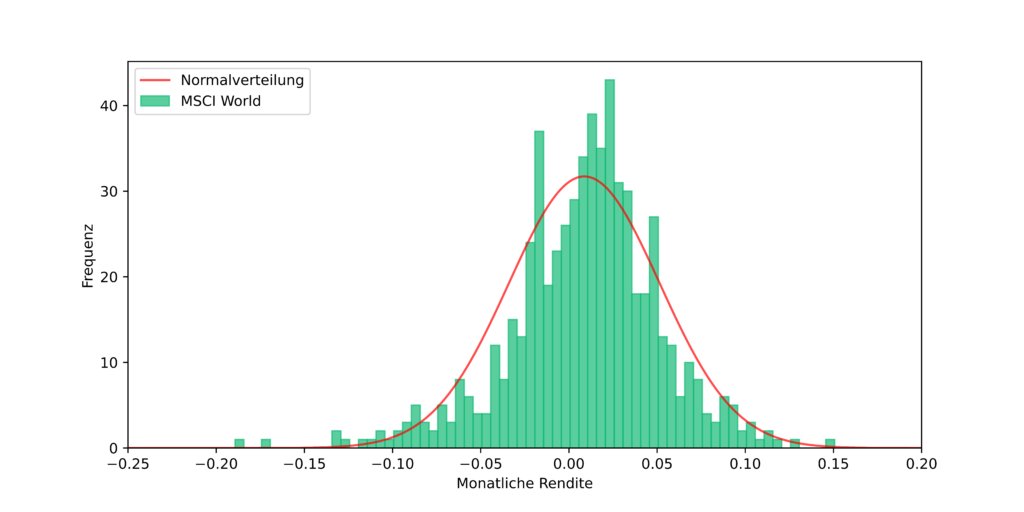
Da stark negative Renditen von der Normalverteilung signifikant unterschätzt werden, verwenden wir einmal die Normalverteilung als Grundlage für die Monte-Carlo-Simulation und einmal die tatsächlichen Renditen. Anhand der Ergebnisse können wir dann einschätzen, ob die Unterpräsentation von drastischen Kurseinbrüchen bei der Normalverteilung einen ausschlaggebenden Einfluss auf die Performance oder das Risiko eines Aktieninvestments hat.

Die Methode der Monte-Carlo-Simulation

Im Rahmen der Monte-Carlo-Simulation besteht jeder mögliche Pfad bzw. jedes Zukunftsszenario aus einer Folge von Zufallsereignissen, die gemäß einer Wahrscheinlichkeitsverteilung gewichtet sind. Bei der Simulation eines Aktienportfolios entsprechen die Zufallsereignisse dem zufälligen Bestimmen einer Rendite. Wir werden uns dabei auf die monatliche Entwicklung der Rendite beschränken und die Entwicklung des Portfolios für einen Zeitraum von 360 Monaten bzw. 30 Jahren betrachten. Für unsere Monte-Carlo-Simulation bedeutet das, dass wir für jeden Pfad 360 monatliche Renditen zufällig gemäß einer der beiden oben beschriebenen Wahrscheinlichkeitsverteilungen generieren müssen.

Bildlich kann man sich den Prozess für die tatsächliche Renditeverteilung des MSCI World wie folgt vorstellen. Die Verteilung der tatsächlichen Renditen, die in Abbildung 1 in grün zu sehen ist, besteht aus 613 monatlichen Renditen. Theoretisch könnte man sich 613 Kugeln besorgen und auf jede dieser Kugeln eine der vergangenen Renditen des MSCI World schreiben. Mit Hilfe einer Lottotrommel könnten wir dann zufällig eine dieser Kugeln ziehen. Nach jedem Ziehvorgang wird die gezogene Kugel wieder zurück gelegt und das Ganze 360 mal wiederholt. Das wäre dann das Ergebnis einer einzigen Monte-Carlo-Simulation. Für die Normalverteilung kann man genauso vorgehen, die Kugeln in der Trommel müssten nur nach der Normalverteilung gewichtet werden.

Wir gehen bei den Simulationen davon aus, dass die Rendite eine unabhängige Größe ist, d.h. die Rendite eines Monats hängt nicht von den Werten der Renditen von vergangenen Monaten ab bzw. es herrschen keine Korrelationen zwischen den Renditen verschiedener Monate. Diese Annahme kann man anzweifeln, wenn man sich beispielsweise einen langanhaltenden sogenannten Bärenmarkt anschaut, bei dem die Kurse konsistent über einen längeren Zeitraum abnehmen. Wie man solche Korrelationen in das Modell einbinden kann und wie sie sich auswirken, werden wir in einem der kommenden Blogeinträge beleuchten.

Da der Prozess mit den Kugeln etwas mühsam und zeitaufwendig wäre, werden wir einen computergestützten Zufallszahlengenerator nutzen, der ebenfalls zufällige Renditen gemäß der beiden Verteilungen generieren kann, dies aber weitaus effizienter realisiert. Insgesamt werden wir für beide Verteilungen jeweils 10 000 Monte-Carlo-Simulationen durchführen, d.h. jeweils 10 000 mögliche Zukunftsszenarien für unser Portfolio erhalten, die sich aus der vergangen Entwicklung des MSCI World ergeben.

Ob sich der MSCI World bzw. die Aktienmärkte im Allgemeinen in der Zukunft ähnlich entwickeln werden wie in der Vergangenheit, kann natürlich kein Mensch wissen. Da wir aber keine anderen Daten haben oder allgemeingültige Gesetzmäßigkeiten bezüglich des Aktienmarkts kennen, liefert die Vergangenheit die einzige Möglichkeit Erkenntnisse zu gewinnen. Und mit der Monte-Carlo-Simulation haben wir ein mächtiges Werkzeug, um mögliche Zukunftsszenarien daraus abzuleiten.

Analyse der Ergebnisse der Monte-Carlo-Simulationen

In diesem Abschnitt werden wir die Ergebnisse der Monte-Carlo-Simulationen betrachten. Dabei legen wir einmal die tatsächlichen historischen Renditen des MSCI World zugrunde und einmal eine daraus abgeleitete Normalverteilung, die zu einer Unterrepräsentation von einschneidenden Ereignisse mit stark negativen Renditen führt.

Animation der Monte-Carlo-Simulation

Um den Prozess der Monte-Carlo-Simulation zu veranschaulichen, könnt ihr hier ein Video mit einer exemplarischen Simulation sehen, der die Normalverteilung zugrunde liegt. Wir starten mit einem Portfoliowert von 100 Geldeinheiten. Auf der linken Seite sieht man die Normalverteilung sowie ein Histogramm der simulierten bzw. zufällig gezogenen Renditen, welches sich mit der Zeit langsam aufbaut. Auf der rechten Seite sieht man die dazugehörige Entwicklung des Portfoliowerts. Mit zunehmender Zeit sieht kann man sehr schön den Zinseszinseffekt beobachten, da er dazu führt, dass der Wert des Portfolios absolut nun viel stärker schwankt als zu Beginn.

Kursentwicklung

In Tabelle 1 sind exemplarische Teilergebnisse der Monte-Carlo-Simulationen mit Normalverteilung zu sehen. Die ganze Tabelle besitzt insgesamt 10 000 Spalten, eine für jedes mögliche Zukunftsszenario und 361 Zeilen, eine für jeden simulierten Monat (die erste Zeile enthält den Startwert des Portfolios). Aus der letzten Zeile ist bereits ersichtlich, dass der Endwert des Portfolios nach 30 Jahren sehr stark schwanken kann.

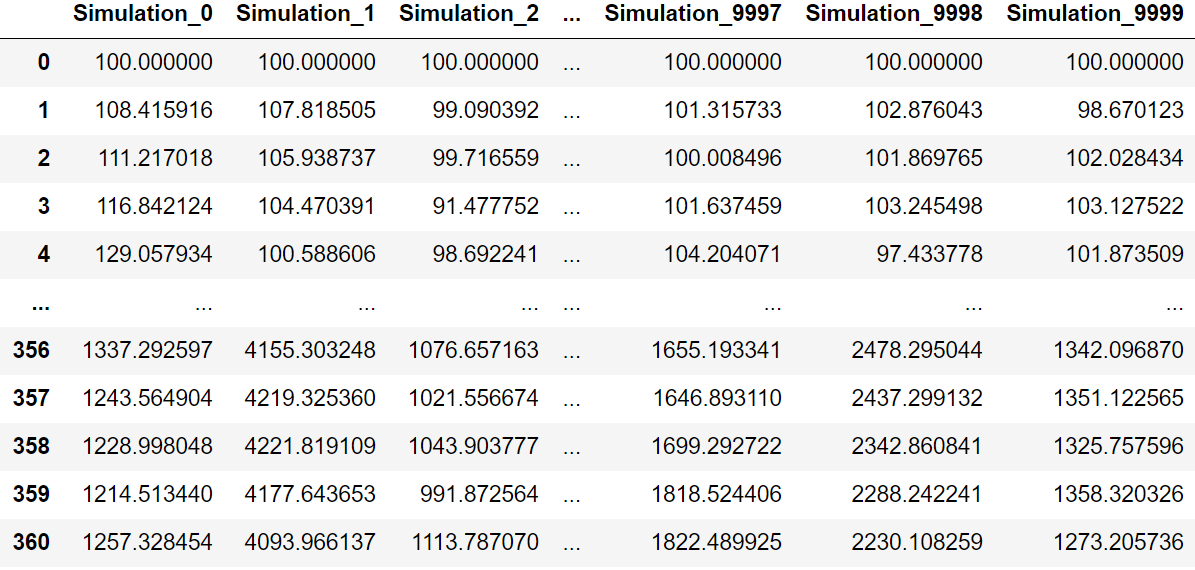
In Tabellenform können wir hier aufgrund der Menge der Datenpunkte natürlich nicht alle Werte darstellen. Um aber einen Gesamteindruck der Ergebnisse aller Simulationen zu erhalten, sind in Abbildung 2 die Werteentwicklungen von allen 10 000 möglichen Zukunftsszenarien dargestellt. Da die Portfoliowerte nach 30 Jahren Zinseszinseffekt beträchtlich angewachsen sein können, haben wir eine logarithmische Skala verwendet, um auch die Entwicklung von sehr schlecht laufenden Portfolios mit geringem absoluten Wert beobachten zu können. In der Animation oben haben wir dagegen eine lineare Skala verwendet. Die Spannweite der Endwerte reicht dabei von mickrigen 70 Geldeinheiten bis zu fast 50 000 Geldeinheiten. Wichtig zu beachten ist, dass es sich hierbei um nominale Werte handelt, die nicht inflationsbereinigt sind.

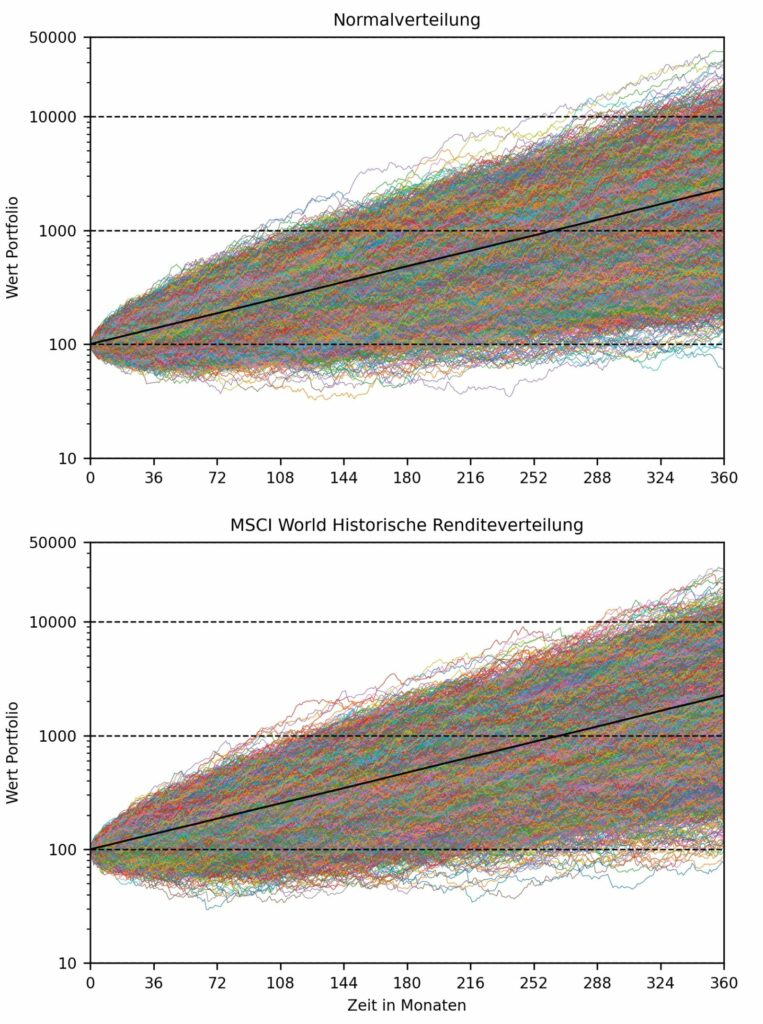
Auf den ersten Blick ist das Gesamtbild aller Simulationen zwischen Normalverteilung und tatsächlicher Renditeverteilung nicht wirklich unterscheidbar, außer dass bei der Verwendung der tatsächlichen Renditen Extremszenarien, bei denen der Portfolioendwert um die 100 Geldeinheiten liegt, häufiger vorkommen. Die schwarze Linie repräsentiert den Durchschnittswert der Portfolios für alle Simulationen zum gegebenen Zeitpunkt. Nach 30 Jahren beträgt er bei der Normalverteilung 2325 Geldeinheiten und bei der tatsächlichen Renditeverteilung 2252 Geldeinheiten. Es gibt also keinen signifikanten Unterschied. Das ist aufgrund der identischen Erwartungswerte beider Verteilungen auch absehbar gewesen.

Da Abbildung 2 mit der Gesamtheit aller Simulationen sehr unübersichtlich ist, betrachten wir im Folgenden ein Histogramm aller Portfoliowerte im Jahr 20, also 240 Monate nach Simulationsbeginn. Das Histogramm ist praktisch ein Schnitt entlang aller Kurse beim Monat 240. Das Ergebnis ist in Abbildung 3 zu sehen.

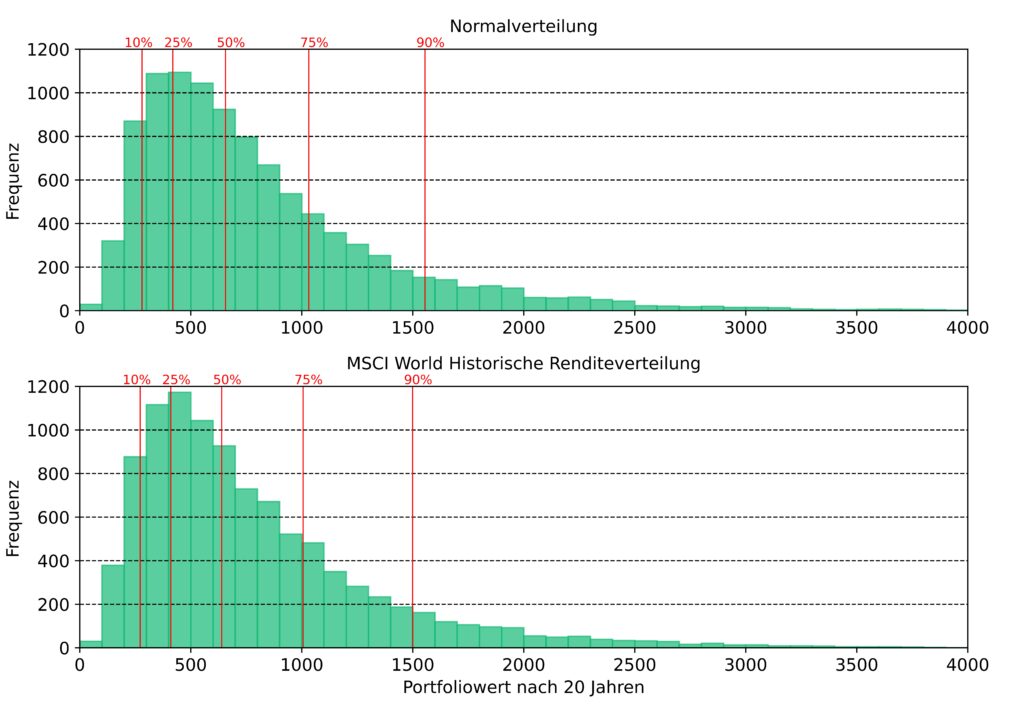
Auf den ersten Blick sehen die Histogramme für Normalverteilung und tatsächliche Renditeverteilung identisch aus. Erst die Quantile zeigen, dass die Portfoliowerte nach 20 Jahren für die tatsächliche Renditeverteilung leicht in Richtung der niedrigeren Werte verlagert ist. Kurz zur Bedeutung von Quantilen. Das 90 %-Quantil besagt zum Beispiel, dass 90 % aller Simulationen im Falle der tatsächlichen Renditeverteilungen einen Portfoliowert von bis zu 1500 Geldeinheiten haben, während dieser Wert bei der Normalverteilung bei ca. 1550 liegt. Der Unterschied zwischen Normalverteilung und tatsächlicher Renditeverteilung ist aber wieder sehr gering.

Maximum Drawdown

Eine weitere Größe, die bei der Beurteilung von Aktieninvestments eine wichtige Rolle spielt, ist der sogenannte Maximum Drawdown. Ein Drawdown (im Deutschen könnte man ihn als Werteverlust bezeichnen) stellt den Verlust zwischen Höchststand und dem darauf folgenden Tiefstand innerhalb einer bestimmten Periode dar. Das Maximum dieser Drawdowns ist dann der Maximum Drawdown.

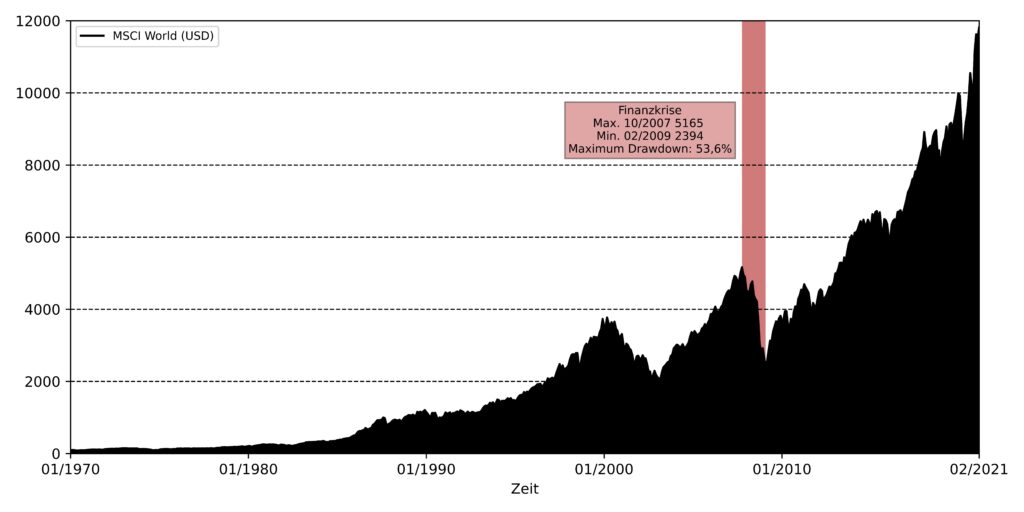
Zur Veranschaulichung der Bedeutung ist in Abbildung 4 der Maximum Drawdown für den MSCI World in den letzten 50 Jahren dargestellt. Er fand zur Zeit der großen Finanzkrise statt, mit dem Höchststand im Oktober 2007 und dem Tiefstand im Februar 2009. Der Maximum Drawdown betrug satte 53,6 %.

Wie verhält sich der Maximum Drawdown für unsere simulierten Szenarien? In Abbildung 5 sind Histogramme für den Maximum Drawdown aller 10 000 Monte-Carlo-Simulationen für die Normalverteilung und die tatsächliche Renditeverteilung zu sehen. Bei genauer Betrachtung kann man erkennen, dass für die tatsächliche Renditeverteilung geringe Maximum Drawdowns bis 37,5 % deutlich weniger häufig vorkommen als bei der Normalverteilung. Das führt dazu, dass der Durchschnitt der Maximum Drawdowns aller Simulationen für die tatsächliche Renditeverteilung um 1,8 Prozentpunkte größer ist.

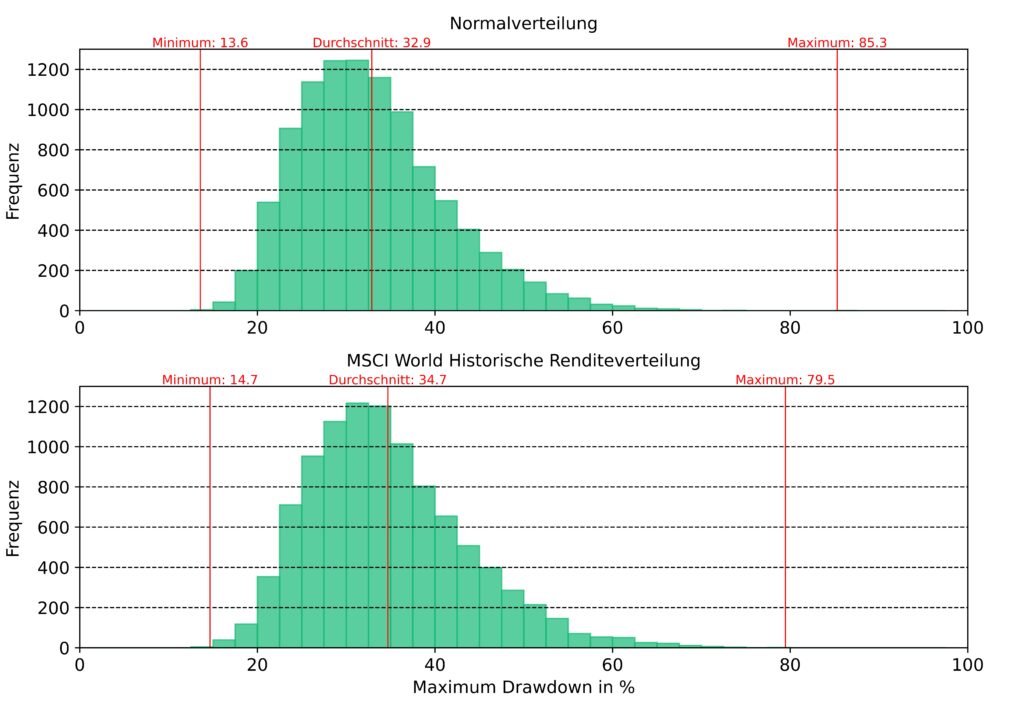
Die Wahrscheinlichkeit für zeitweise höhere Werteverluste ist somit bei der tatsächlichen Renditeverteilung höher als bei der Normalverteilung. Dies steht im Einklang mit der Unterrepräsentation von Ereignissen mit stark negativen Renditen in der Normalverteilung. Der Maximum Drawdown nimmt für Anleger in psychologischer Sicht eine wesentliche Rolle ein. Kein Anleger sieht gerne ein Minus von -50 % in seinem Depot und es besteht die Gefahr, dass der Anleger diese Verluste durch einen Verkauf dann auch tatsächlich realisiert. Nicht umsonst ist die Anzahl der deutschen Aktienanleger im Zuge der Dotcom-Blase und der großen Finanzkrise stark gesunken. [4]

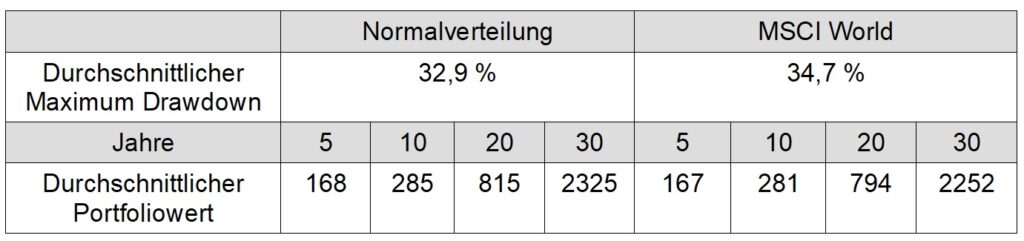
In Tabelle 2 sind die durchschnittlichen Portfoliowerte nach 5, 10, 20 und 30 Jahren sowie der Maximum Drawdown der Monte-Carlo-Simulationen für Normalverteilung und tatsächlicher Renditeverteilung des MSCI World zusammengefasst.

Fazit

• In diesem Artikel haben wir uns mit Monte-Carlo-Simulationen für Aktienportfolios beschäftigt und untersucht, ob sich die Ergebnisse unterscheiden, je nachdem ob die tatsächliche Renditeverteilung oder eine Normalverteilung verwendet wird.
• Aus Tabelle 2 ist ersichtlich, dass die Portfoliowerte und die korrespondierenden Quantile zu verschiedenen Zeitpunkten keine substanziellen Unterschiede aufweisen.
• Die einzige Größe, die einen signifikanten Unterschied aufweist, ist der Maximum Drawdown, dessen Durchschnittswert für die tatsächliche Renditeverteilung um 1,8 Prozentpunkte größer ist und hohe zeitweise Verluste häufiger vorkommen.
• Zu Beginn haben wir bereits erwähnt, dass wir bei unseren Monte-Carlo-Simulationen davon ausgehen, dass die monatlichen Renditen unabhängig voneinander sind. Da wir in der Vergangenheit jedoch langanhaltende Bären- und Bullenmärkte beobachten konnten, stellt sich die Frage in wie weit vergangene Renditen und zukünftige Renditen miteinander korrelieren. Dazu werden wir uns in einem kommenden Blogartikel mit der Verteilung der zeitlichen Länge von bestimmten Börsenphasen beschäftigen. Wir werden untersuchen, ob diese mit einer unabhängigen Verteilung der Renditen reproduziert werden können oder ob man unsere einfache Monte-Carlo-Simulation um Korrelationen erweitern muss. Folgt beispielsweise auf eine negative Rendite mit 50 % Wahrscheinlichkeit erneut eine negative Rendite?
• Ein empfehlenswertes Buch zum Thema Monte-Carlo-Simulationen für Portfolios und die Rolle des Zufalls im Leben ist das Buch „Narren des Zufalls“ (engl. Original „Fooled by Randomness“) vom Autor Nassim Nicholas Taleb (siehe Buchtipps für mehr Informationen).
• Es gibt im Internet Tools mit denen man Monte-Carlo-Simulationen für Aktienportfolios einfach online durchführen kann. Für nähere Informationen siehe Finanztools.

Habt ihr schon einmal die Monte-Carlo-Simulation genutzt, um mögliche Zukunftsszenarien für euer Aktienportfolio, eure ETF-Sparpläne oder Entnahmepläne zu simulieren? Lasst es mich in den Kommentaren wissen.

Quellen und empfehlenswerte Literatur

[1]: Metropolis, N. C./Ulam, S. (1949): The Monte Carlo Method, Journal of the American Statistical Association, Vol. 44, No. 247, (Sep. 1949), S. 335-341.

[2]: Cootner, Paul H. (1964). The Random Character of Stock Market Prices

[3]: Lo, Andrew (1999). A Non-Random Walk Down Wall Street

[4]: Deutsches Aktieninstitut (2019). Deutsche Aktionärszahl